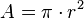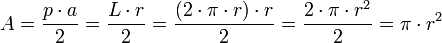- Afianzar el concepto de ecuación de una circunferencia .
- Practicar el paso de la ecuación general a la ecuación reducida.
- Estudiar la posición relativa de una recta y una circunferencia dibujando sus gráficas y resolviendo el sistema de sus dos ecuaciones.
- Estudiar la posición relativa de dos circunferencias dibujando sus gráficas y resolviendo el sistema de sus dos ecuaciones.
- Analizar la tangencia de circunferencias .
lunes, 19 de septiembre de 2011
Objetivos
Introduccion
La circunferencia es una línea curva, plana y cerrada, cuya definición más usual es:
Una circunferencia es el conjunto de todos los puntos de un plano que equidistan de otro punto fijo y coplanar llamado centro. |
Marco Teòrico Referencial
http://es.wikipedia.org/wiki/Circunferencia
http://html.rincondelvago.com/circunferencia.html
http://www.dav.sceu.frba.utn.edu.ar/homovidens/chavezalejandro_mattje/trabajofinal/paginas/inicio.htm
http://recursostic.educacion.es/descartes/web/materiales_didacticos/circunferencia_ppc/inicio_circunferencia.htm
http://html.rincondelvago.com/circunferencia.html
http://www.dav.sceu.frba.utn.edu.ar/homovidens/chavezalejandro_mattje/trabajofinal/paginas/inicio.htm
http://recursostic.educacion.es/descartes/web/materiales_didacticos/circunferencia_ppc/inicio_circunferencia.htm
Proceso
Elementos de la circunferencia
Existen varios puntos, rectas y segmentos, singulares en la circunferencia: La mediatriz de una cuerda pasa por el centro de la circunferencia.
La mediatriz de una cuerda pasa por el centro de la circunferencia.
- Centro, el punto interior equidistante de todos los puntos de la circunferencia;
- Radio, el segmento que une el centro con un punto cualquiera de la circunferencia;
- Diámetro, el mayor segmento que une dos puntos de la circunferencia (necesariamente pasa por el centro);
- Cuerda, el segmento que une dos puntos de la circunferencia; (las cuerdas de longitud máxima son los diámetros)
- Recta secante, la que corta a la circunferencia en dos puntos;
- Recta tangente, la que toca a la circunferencia en un sólo punto;
- Punto de tangencia, el de contacto de la recta tangente con la circunferencia;
- Arco, el segmento curvilíneo de puntos pertenecientes a la circunferencia;
- Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.
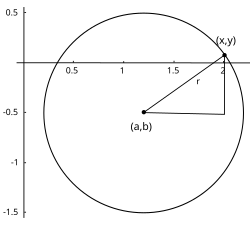
En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación
 .
.
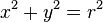 .
.
De la ecuación general de una circunferencia,
 ,
,la ecuación de la circunferencia es:
[editar] Ecuación vectorial de la circunferencia
La circunferencia con centro en el origen y radio R, tiene por ecuación vectorial: . Donde
. Donde  es el parámetro de la curva, además cabe destacar que
es el parámetro de la curva, además cabe destacar que 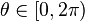 . Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
. Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.[editar] Ecuación en coordenadas polares
Cuando la circunferencia tiene centro en el origen y el radio es c, se describe en coordenadas polares como
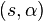 y el radio es
y el radio es  , la ecuación se transforma en:
, la ecuación se transforma en:[editar] Ecuación en coordenadas paramétricas
La circunferencia con centro en (a, b) y radio c se parametriza con funciones trigonométricas como:[editar] Área
Artículo principal: Área de un círculo
El área del círculo delimitado por la circunferencia es: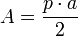 .
.Considerando la circunferencia como el caso límite de un polígono regular de infinitos lados, entonces, el apotema coincide con el radio, y el perímetro con la longitud de la circunferencia, por tanto:
Conclusiones
Conclusión
La Circunferencia es un elemento geométrico de mucha importancia. Esta muy a diario en todas partes, gracias a este se pueden realizar muchas técnicas de gran precisión con productos como los Esferas en general etc.
Bibliografia
http://es.wikipedia.org/wiki/Circunferencia
http://html.rincondelvago.com/circunferencia.html
http://www.dav.sceu.frba.utn.edu.ar/homovidens/chavezalejandro_mattje/trabajofinal/paginas/inicio.htm
http://recursostic.educacion.es/descartes/web/materiales_didacticos/circunferencia_ppc/inicio_circunferencia.htm
http://html.rincondelvago.com/circunferencia.html
http://www.dav.sceu.frba.utn.edu.ar/homovidens/chavezalejandro_mattje/trabajofinal/paginas/inicio.htm
http://recursostic.educacion.es/descartes/web/materiales_didacticos/circunferencia_ppc/inicio_circunferencia.htm
Suscribirse a:
Entradas (Atom)



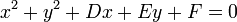







![x=a + c \cos t,\ y=b+c\sin t,\qquad t\in[0,2\pi]](http://upload.wikimedia.org/math/f/d/0/fd08b31a7dac369664c95f143fb10657.png)